1. Principe
2. Approches
   1. Distance d’édition
   2. Enumération des éditions possibles
   3. Arbre n-aire
      1. Déplacement dans l’arbre : sans éditions
      2. Déplacement dans l’arbre : éditions
      3. Conclusion sur l’utilisation d’un arbre n-aire
3. Code
   1. La méthode find_closest
   2. La méthode _find_closest
      1. Les set
      2. Avancer dans l’arbre : sans éditions
      3. Avancer dans l’arbre : avec éditions
         1. Délétions et Subsitutions
         2. Insertions et Transpositions
4. Pour aller plus loin
5. Conclusion

Les correcteurs orthographiques sont de petits programmes qui permettent de détecter les mots mal orthographiés et permettent de suggérer à l’utilisateur des propositions de correction. Comme les programmes d’auto-complétion, ils sont intégrés dans de nombreux programmes (traitement de texte, IDE, etc.). Nous allons ici réaliser un correcteur orthographique simple en utilisant un arbre n-aire. Etant donné que nous avons déjà réalisé un programme utilisant un arbre n-aire (voir supra), je ne redétaillerai pas la terminologie utilisée ni les parties du programme déjà détaillées dans l’article précédent.

Principe

L’idée d’un correcteur orthographique est ① d’identifier les mots mal orthographiés et ② de rechercher les mots qui ont la distance d’édition la plus proche possible des mots mal orthographiés. La distance d’édition est une mesure qui indique le nombre d’opérations de substitution (1 pour « abocat » → « avocat »), de délétion (1 pour « avvocat » → « avocat ») et d’insertion (« aocat » → « avocat ») réunies qu’il faut pour transformer le mot fautif en un mot correct. On peut également rajouter une autre opération, la transposition (« aovcat » → « avocat ») qui remplace le couple d’opérations insertion + substitution : « aovcat » → « avovcat » (insertion de « v ») → « avocat » (délétion de « v »).

Identifier des mots mal orthographiés est facile, il suffit de regarder si les mots existent où non dans la structure de données que nous utilisons. L’étape la plus compliquée est de rechercher des mots qui ont la distance d’édition la plus proche possible.

Approches

Distance d’édition

La première solution consiste à calculer la distance d’édition entre le mot mal orthographié et chacun des mots de la structure de données, et ne conserver que les mots pour lesquels la distance est en dessous d’un seuil défini par l’utilisateur. Cependant, cette solution est extrêmement coûteuse puisqu’elle implique de calculer une distance d’édition pour chacun des mots de la structure de données. De plus, calculer une distance d’édition — en utilisant par exemple la distance de Levenshtein — est également une opération qui peut être relativement coûteuse. Ainsi, cette approche est peu efficace.

Enumération des éditions possibles

Dans cette approche, on génère l’ensemble des éditions possibles à partir du mot mal orthographié et on filtre la liste générée pour ne garder que les mots qui existent. C’est l’option adoptée par Peter Norvig dans son implémentation. Imaginons que le mot mal orthographié est « aovcat », nous allons partir de celui-ci et générer l’ensemble de insertions, délétions, substitutions et transpositions possibles :

• Pour les insertions nous avons ['aaovcat', 'baovcat', ..., 'uavocat', ..., 'aovcatz']
• Pour les délétions nous avons ['ovcat', 'avcat', 'aocat', ..., 'aovca']
• Pour les substitutions nous avons ['aovcat', 'bovcat', 'covcat', ..., 'aovcaz']
• Pour les transpositions nous avons ['oavcat', 'avocat', 'aocvat ', ..., 'aovcta']

L’intuition de cette approche est que l’on espère que l’une des opérations d’insertion, délétion, substitution et transposition génèrera le mot correct. C’est d’ailleurs le cas si le mot erroné a une distance d’édition de 1 avec le mot correct. Il suffit simplement de filtrer la liste pour ne garder que les mots qui existent (ainsi on supprime « aaovcat », « oavcat », etc.) et l’on conserve pour finir seulement le mot correct « avocat » (ici, généré par l’opération de transposition). Si l’on souhaitait pouvoir récupérer la correction d’un mot qui contiendrait 2 erreurs, il faudrait générer l’ensemble des éditions possibles (insertions, délétions, substitutions et transpositions) de l’ensemble des mots que l’on aurait déjà générés via cette même opération.

La solution proposée par Norvig repose sur l’utilisation d’un alphabet pour savoir quels caractères insérer ou substituer (letters = 'abcdefghijklmnopqrstuvwxyz'). Cela n’est pas idéal, car l’alphabet ne fonctionne que pour la langue pour laquelle le programme a été conçu. Ainsi, si l’on souhaitait travailler sur du français, il serait nécessaire d’ajouter de nouveaux caractères (« é », « è », « ù », etc.). On pourrait aisément résoudre ce problème en ne considérant que les caractères contenus dans le dictionnaire d’entrée.

Cependant, cette approche par liste de caractères se révèle problématique à un autre niveau. Plus il y a de caractères à considérer, plus il y a de d’insertions et de substitutions possibles. Si l’on considère un alphabet de 26 lettres, pour chaque mot mal orthographié de n caractères, le programme génèrera :

• n+1 * 26 insertions
• n délétions
• n * 26 substitutions
• n-1 transpositions
• Total : 53n + 25 possibilités

en supposant que l’alphabet que l’on considère pour l’insertion et la substitution de caractère est composé de 26 lettres (et ce, juste pour trouver l’orthographe correcte de mots qui n’ont une distance d’édition de 1 avec le mot correct !). Ainsi, on constate ici un double effet : plus le mot sera long et plus l’on considérera de lettres dans l’alphabet, plus il y aura de propositions à filtrer. Imaginez si l’on prend en plus en compte les lettres majuscules !

Cette solution n’est pas optimale pour une autre raison également. Par exemple, on sait que des mots qui commencent par « ua » (comme dans l’option générée par l’opération d’insertion) sont des mots plutôt rares (voire inexistants) en français. On aimerait donc pouvoir générer seulement des éditions qui soient possibles en français, ce qui nous permettra d’éliminer d’office beaucoup de noms impossibles. De la même manière, l’approche par alphabet nous oblige à considérer des lettres qui sont extrêmement rares en français pour des substitutions ou insertions que l’on sait peu probables. Par exemple en français, nous sommes obligés de considérer la lettre « ÿ » (qui apparaît dans quelques noms de villes comme Aÿ ou L’Haÿ-les-Roses) et qui sera utilisée pour chacune des insertions et substitutions, quel que soit le mot.

Arbre n-aire

Je vais vous proposer ici d’implémenter un correcteur orthographique qui fonctionne avec un arbre n-aire. Conceptuellement, l’approche est proche de celle de Norvig (cf. supra). Cependant, ici nous allons tâcher de filtrer les propositions de correction le plus tôt possible et nous n’allons considérer que les lettres qui sont possibles à moment t — qui dépend de l’endroit où nous sommes dans le mot — pour les insertions et substitutions.

Pour illustrer ce dernier point, imaginons que l’utilisateur ait mal orthographié le mot « coquelicot » en écrivant « coqueliot ». Pour corriger ce mot, il suffit de rajouter le « c » entre le « i » et le « o » . Imaginons que nous ayons lu les c premiers caractères du mot et sommes arrivés au caractère « i ». Si l’on faisait une implémentation à la Norvig, on testerait ici plusieurs possibilités d’insertion « a » pour « coqueliaot », puis « b », puis « c » le tout jusqu’à « z » pour « coquelizot ». Or, en français (en tous cas, d’après la liste de mot de Lexique v3.83), la seule lettre possible après le « i » ici est le « c ». Inutile donc de considérer toutes les autres lettres à l’exception du « c » pour corriger le mot. C’est donc ce que nous allons faire !

Déplacement dans l’arbre : sans éditions

Pour bien comprendre intuitivement ce que nous allons implémenter, il convient de bien comprendre comment l’on peut se déplacer de nœud en nœud dans l’arbre. C’est ce qu’illustre la figure suivante :

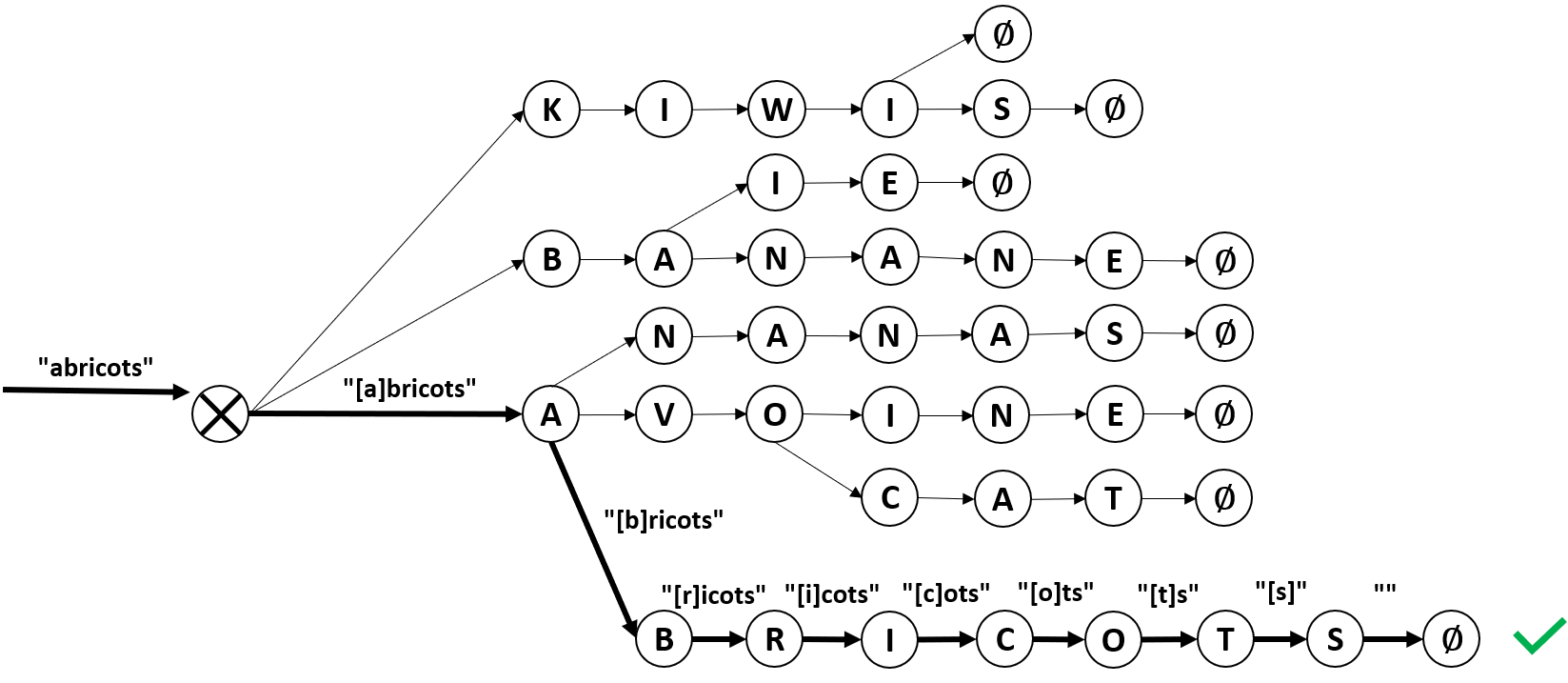
Les flèches en gras noires figurent le chemin emprunté. Le mot en gras est l’état de la chaîne avant le déplacement d’un nœud à l’autre et les lettres entre crochets indiquent le caractère qui permet de passer d’un nœud à l’autre. Ainsi, pour se déplacer de nœud en nœud, on regarde le premier caractère de la chaîne, si celui-ci correspond à l’étiquette d’un des nœuds fils du nœud sur lequel on est, on peut se déplacer sur celui-ci, puis l’on examine le caractère suivant, etc. Si après avoir consommé tous les caractères on est arrivé sur un nœud marquant la fin d’un mot ∅, c’est que le mot initial était bien un mot existant. Si cette opération de déplacement est floue, n’hésitez pas à lire cet article avant où j’aborde l’opération plus en détail.

Déplacement dans l’arbre : éditions

Maintenant que nous avons compris comment nous déplacer dans l’arbre lorsque le mot rentré existe effectivement dans l’arbre, nous allons voir comment utiliser l’arbre pour générer des éditions lorsque le mot rentré est mal orthographié, ce qui nous permettra finalement de trouver sa correction. Ici, nous n’allons autoriser qu’une seule édition — quelle qu’elle soit : insertion, délétion, substitution ou transposition.

• Délétion et Substitution

Voyons comment nous pouvons corriger le mot « avoat » en « avocat » (où l’utilisateur a oublié la lettre « c » donc) :

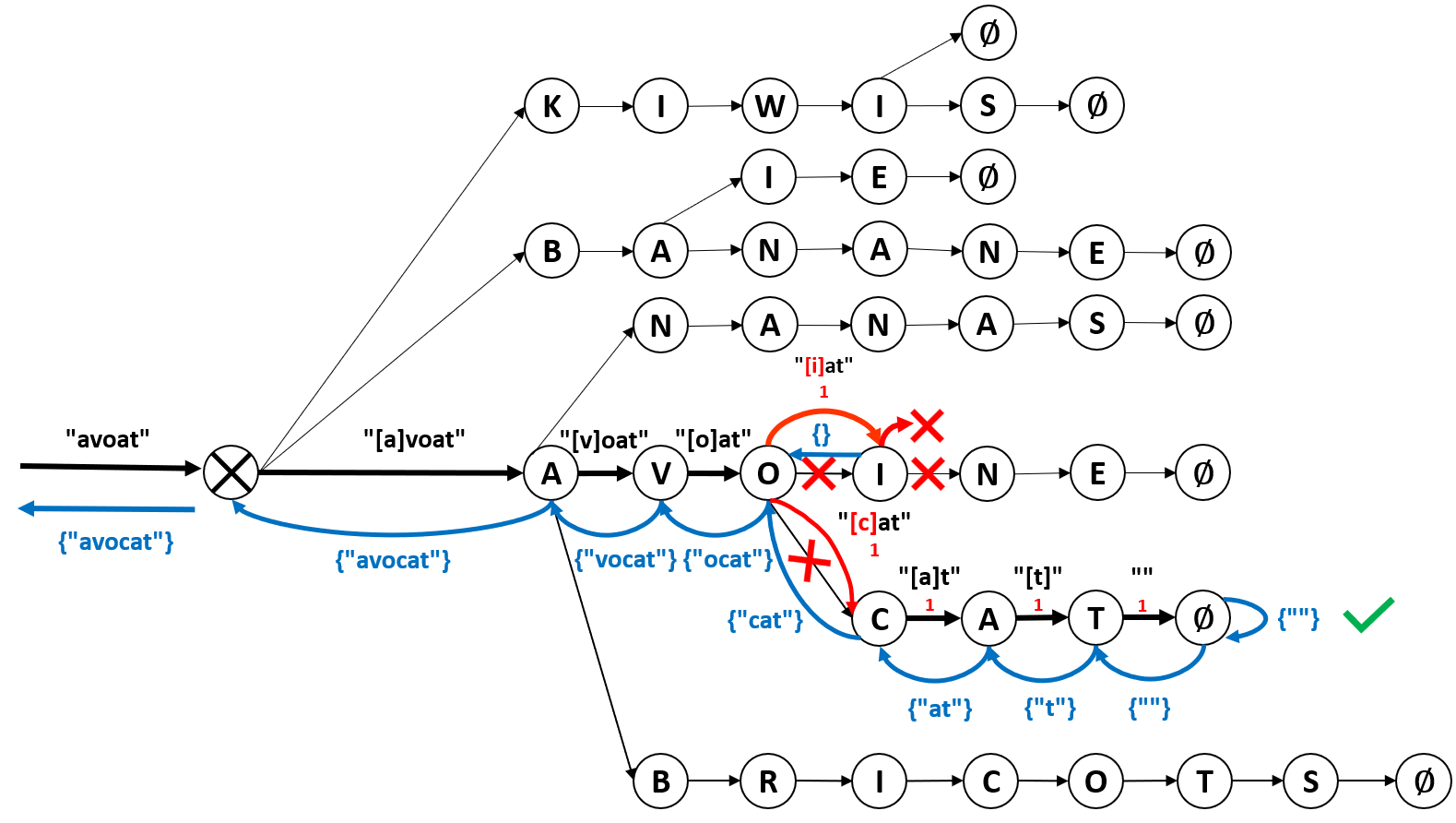
Comme dans la précédente figure, les flèches en gras noires figurent le chemin « normal », le mot en gras est l’état de la chaîne avant le déplacement d’un nœud à l’autre et les lettres entre crochets indiquent le caractère qui permet de passer d’un nœud à l’autre.

Au début, il n’y a aucun problème et on peut aller de nœud en nœud dans l’arbre jusqu’au nœud « o ». Arrivés sur ce nœud, la chaîne qu’il nous reste à parcourir est « at » ; cependant, à partir du nœud « o » il n’y a aucun nœud « a » sur lequel nous pourrions aller. Ainsi, pour passer au nœud suivant, nous allons nous autoriser à faire une insertion (pour corriger la délétion accidentelle de l’utilisateur). Pour ce faire, nous allons nous autoriser à aller sur tous les nœuds fils du nœud « o », c’est à dire ici « i » et « c ». Cependant, nous ne pouvons pas aller par la voie normale (flèches noires marquées d’un ❌) sinon il aurait fallu que le reste de la chaîne commence soit par « i » soit par « c ». Au lieu de cela, nous passons par les voies rouges, ce qui reviendra par la suite à rajouter la lettre manquante. Nous indiquons à partir de là, sous la chaîne de caractères, le nombre d’éditions que nous avons apportées (ici 1).

A partir de là, nous arrivons sans problème à parcourir le reste de la chaîne « at » pour la branche du dessous (✔️) et arrivons sur la fin de mot ∅ . Pour la branche du dessus, nous voyons que nous sommes bloqués : dans le cas de la flèche noire avec ❌ parce que la chaîne « at » qu’il reste à consommer commence par « a » et le seul nœud accessible depuis le nœud « i » est le nœud « n » ; et dans le cas de la flèche rouge avec ❌parce que nous ne pouvons plus faire d’édition (je vous rappelle que nous avons défini que le nombre maximal d’éditions serait de 1). Il est à noter que si l’utilisateur avait substitué une lettre par une autre (par exemple « avacat »), nous aurions effectué la même opération.

Une fois arrivés à la fin d’un mot, comme dans le cas de la branche du dessous, nous allons maintenant remonter vers la racine de l’arbre (chemin indiqué en bleu). Cette opération est facile (et se fait de la même manière que pour l’auto-complétion) et nous permet de reconstruire le mot corrigé. Ainsi, arrivés sur le nœud « c » lors du retour, nous remontons vers le nœud « o », et c’est lors de cette étape que nous « rajoutons » la lettre « c » qui était manquante de l’entrée de l’utilisateur.

• Insertion et Transposition

Dans le cas d’une insertion ou d’une transposition, l’arbre est relativement similaire. Cependant, là où dans le cas de la délétion ou de la substitution nous nous autorisions à passer à l’ensemble des nœuds fils d’un nœud donné sans toucher à la chaîne de caractères, dans le cas d’une insertion ou d’une transposition nous allons nous autoriser à modifier la chaîne de caractères. Dans la figure ci-dessous, nous voyons le cas où l’utilisateur aurait inséré une lettre en trop : ici « d » dans « avodcat ».

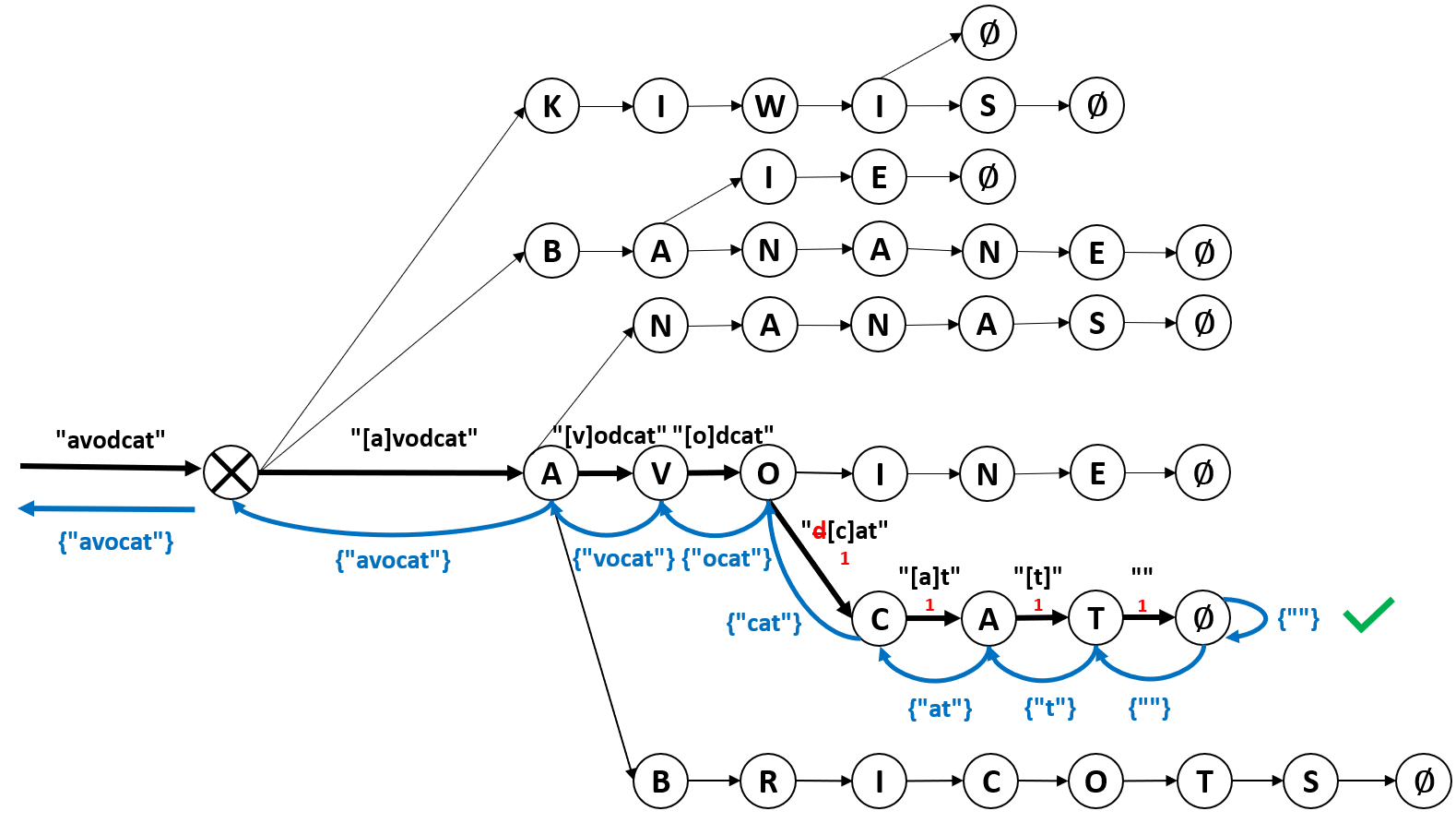
Comme pour l’exemple précédent, nous arrivons sur le nœud « o » sans problème. La chaîne qu’il reste est « dcat », mais il n’y a cependant pas de nœud « d » lié au nœud « o ». Nous nous autorisons ici à éditer la chaîne en retirant la lettre « d ». Une fois cette chaîne modifiée, la nouvelle lettre du début devient « c », ce qui nous autorise à aller sur le nœud suivant et finalement atteindre la fin du mot. Si la première lettre n’avait pas permis d’aller sur un autre nœud, nous nous serions dans ce cas arrêtés, ne pouvant plus faire d’autres éditions (car nous avons défini le nombre d’éditions maximum à 1).

Dans le cas d’une transposition, par exemple « avcoat », une fois arrivés sur le nœud « c » nous aurions regardé s’il ce nœud avait pour fils la deuxième lettre de la chaîne restant à traiter (« c[o]at »), et si tel avait été le cas, nous aurions inversé les deux premières lettres (« coat » → « ocat ») pour nous permettre d’aller plus loin.

Conclusion sur l’utilisation d’un arbre n-aire

Nous voyons ainsi que l’utilisation d’un arbre n-aire nous permet de faire des éditions au moment ou celles-ci sont possibles (notamment dans le cas de l’insertion et de la substitution).

Il y a un point que je n’ai pas abordé dans les points précédents : ceux-ci peuvent laisser croire que nous appliquons un seul type d’édition (soit insertion, soit substitution, soit délétion, soit transposition) à un moment donné. Or, en réalité, à chaque étape nous appliquons tous les types d’édition possibles. En effet, lorsqu’un mot est erroné, nous ne savons a priori pas où l’erreur a été faite, ni quel est le type d’erreur qui a été fait. Par exemple, si l’utilisateur écrit « Je mange une poime », « poime » peut être corrigé soit en « poire » soit en « pomme », les deux étant possibles, les erreurs n’étant simplement pas au même endroit.

Ainsi, comme pour Norvig, nous faisons toutes les éditions possibles. Cependant, la plupart ne permettront pas d’aller explorer l’arbre très loin et seront donc vite éliminées. Nous pouvons noter que nous générons tout de même moins d’éditions que Norvig, car nous n’explorons que les éditions possibles pour un nœud donné.

Code

Maintenant que nous avons vu comment nous allions appliquer les corrections en utilisant un arbre n-aire, il est venu le moment de le coder ! Le code complet contient trois fichiers interface.py, trie.py et main.py. Nous n’allons détailler que le code de trie.py celui-ci étant au cœur de l’application. Quant à interface.py et main.py, tous deux sont en très grande partie identiques à ceux de programmes d’auto-complétion.

C’est également le cas pour le code de trie.py. Pour rappel, voici le code de base de ce fichier :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

class Trie:

    def __init__(self, end='', words=None):
        """
        Initialisation de l'objet (rappel en Python, le constructeur est __new__)
        :param end: signe de fin de mot à utiliser
        :param words: liste des mots à ajouter au
        """
        self.root = {}
        self.end  = end
    
        if words != None:
            self.add_words(words)
    
    def add_word(self, word):
        """
        Permet d'ajouter UN mot au Trie
        :param word: chaine de caractères
        :return: void
        """
        trie = self.root
        for letter in word:
            trie = trie.setdefault(letter, {})
        trie[self.end] = {}
    
    def add_words(self, words):
        """
        Permet d'ajouter DES mots au Trie
        :param words: liste de chaines de caractères
        :return: void
        """
        for word in words:
            self.add_word(word)

La classe Trie a donc deux attributs root qui représente le nœud racine de l’arbre, et end qui contient le caractère qui sera utilisé pour signaler une fin de mot. Ici, j’ai opté pour une chaine vide. Nous avons également deux méthodes : add_words qui prend en paramètre une liste de mot et qui fait appel à la méthode add_word qui elle prend en paramètre une chaîne de caractères (un mot) qui sera ajouté à l’arbre. Je passe rapidement sur ces points qui sont détaillés ici](/resources/educational/algorithmes-arbres-n-aires-autocompletion/){:target=”_blank”}.

La méthode find_closest

Nous allons créer la méthode find_closest qui aura deux arguments, dont un optionnel : un argument word qui sera le mot rentré par l’utilisateur, et un argument edit_dist qui spécifiera le nombre maximal d’éditions que l’on pourra apporter pour corriger un mot. Par défaut, ce nombre sera fixé à 3. Cette fonction renverra la liste des mots qui sont des corrections potentielles du mot passé en entrée. Il est à noter que nous ne prenons pas ici le temps de vérifier si le mot rentré par l’utilisateur est erroné (alors que l’on ferait dans un cas réel). Vous pouvez cependant prendre le temps de le faire si vous le souhaitez (en rajoutant par exemple une méthode __contains__ qui sera chargée de vérifier si le mot existe).

En réalité, la méthode find_closest va être relativement dépouillée, car elle va faire appel à une fonction imbriquée, c’est-à-dire qu’elle fera appel à une fonction définie à l’intérieur d’elle-même :

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def find_closest(self, word, edit_dist=3):
"""
Retrouve la liste des mots les plus proches du mot `word` (en termes de distance d'édition) dans le trie
:param edit_dist: nombre d'éditions maximum
:param word: mot à corriger
:return: set de mots éloignés d'au plus `edit_dist` éditions du mot `word`
"""

    def _find_closest(trie, edit_dist, word):
        corrections = set()
        
        return corrections
    
    return _find_closest(self.root, edit_dist, word)

Nous voyons donc une méthode find_closest qui a bien deux arguments comme prévu. Cependant, on voit dans le corps de celle-ci la déclaration d’une autre fonction _find_closest. Pourquoi procéder ainsi ? On voit que cette dernière prend un argument de plus que find_closest, en l’occurrence l’argument trie. On voit que la fonction principale, elle, se contente de retourner ce que _find_closest retournera en faisant un return _find_closest(self.root, edit_dist, word) à la ligne 14.

J’ai procédé ainsi, car cela permet d’avoir une interface plus simple pour l’utilisateur. En effet, si nous n’avions pas fait cela, c’est directement find_closest qui aurait eu besoin d’avoir le paramètre trie. Ainsi, l’appel pour l’utilisateur n’aurait pas été très simple à faire et il aurait eu à écrire une ligne de ce type dans le main.py : trie.find_closest(trie.root, "mot_a_corriger"). Cela viole le principe d’encapsulation, l’utilisateur n’ayant pas à savoir le fonctionnement interne d’un objet Trie. En procédant comme je le propose, l’utilisateur n’a plus qu’à écrire trie.find_closest("mot_a_corriger") et n’a pas à se soucier de comment se nomme la racine (ce qui ne l’intéresse de toute façon pas, tout cela relevant des rouages internes de l’application).

La méthode _find_closest

Ainsi, le cœur de find_closest est _find_closest que nous allons maintenant détailler.

Les set

On voit dans le code précédent (ligne 10) que l’on déclare un set nommé corrections qui, comme son nom l’indique, servira à stocker les corrections possibles du mot passé en paramètre puis les retournera (ligne 12). Pourquoi utiliser un set plutôt qu’une liste par exemple ? Un set (un ensemble en français) est une structure de données qui ne permet pas d’avoir des doublons. Ainsi, tous les éléments d’un set sont uniques. Les set ont d’autres propriétés, comme le fait que les éléments n’y soient pas ordonnés, et qu’il n’est pas possible d’y accéder par un indice, comme on le ferait avec une liste. Les set sont d’un point de vue de l’implémentation et du comportement assez proches des dictionnaires — où les éléments seraient les clefs et auxquels on attribuerait une valeur fictive. C’est d’ailleurs un des moyens d’émuler des set pour des langages qui n’ont pas de telle structure de données, comme en feu PHP5 ou en Perl.

Donc, pourquoi utiliser un set ? On utilise un set, on l’a dit, pour retirer d’éventuels doublons. Pourquoi peut-il y avoir des suggestions en double, voire triple ? Il peut y avoir plusieurs suggestions en double car plusieurs éditions différentes peuvent mener à la même correction. Imaginons que nous ayons autorisé une distance d’édition de 2, et que le mot mal orthographié est « pêhce» au lieu de « pêche ». On peut voir deux manières de le corriger :

• la première est de considérer que dans « pêhce » les caractères « c » et « h » ont été transposés. Ainsi, pour corriger ce mot, il suffit d’appliquer une transposition pour inverser le « c » et le « h » et obtenir « pêche »
• la seconde est toujours de considérer qu’il y a bien une transposition, mais qu’au lieu de la corriger par une autre transposition, on la corrige par une délétion suivie d’une insertion (« pêhce » → « pêce » ① → « pêche » ② ou « pêhce » → « pêhe » ① → « pêche » ②), ou d’une insertion suivie d’une délétion (« pêhce » → « pêhche » ① → « pêche » ② ou « pêhce » → « pêchce » ① → « pêche » ②). Ainsi, on voit que le couple insertion/délétion peut engendrer la même correction selon l’ordre dans lequel ils sont enchaînés et le caractère sur lequel ils opèrent en premier.

Ainsi, l’utilisation de set nous permet de retirer les doublons qui pourraient survenir dans le cas où des éditions différentes convergeraient vers la même solution.

Avancer dans l’arbre : sans éditions

Nous allons commencer par la partie la plus simple. Nous allons avancer dans l’arbre sans appliquer d’édition.

1
2
3
4
5
6
7

letter, end = word[0:1], word[1:]
if letter in trie:
    no_editions = _find_closest(trie[letter], edit_dist, end)
    corrections.update(map(lambda t: (letter + t[0], t[1]), no_editions))

if word == '' and trie == {}:
    corrections.update(set({("", 0)})) # str: "word", int: edit_distance

• Nous commençons à la ligne 1 par séparer la première lettre du reste du mot.

  Vous pouvez noter que j’utilise les slice (p.ex. word[2:3]) pour isoler la première lettre (word[0:1]) du reste du mot (word[1:]) au lieu de l’indice du caractère dans la chaîne (p. ex. word[0]). En effet, s’il n’y a pas de caractère à l’indice précisé, Python lèvera une exception ; alors que lorsque l’on passe par des slices Python ne lèvera aucune exception. (‘Attempting to use an index that is too large will result in an error’ et ‘Degenerate slice indices are handled gracefully: an index that is too large is replaced by the string size, an upper bound smaller than the lower bound returns an empty string.’ la dernière phrase étant une phrase que l’on retrouve dans les vieilles documentations de Python). Ce nous évite donc d’avoir à utiliser des if/else ou try/catch :

1
2
3
4
5
6

>>> a = "test"
>>> a[5]
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
IndexError: string index out of range
>>> a[5:1]

• La ligne 3 no_editions = _find_closest(trie[letter], edit_dist, end) nous permet d’avancer de nœud en nœud dans l’arbre. A partir du nœud sur lequel nous sommes (trie), nous avançons vers le nœud suivant trie[letter] si (ligne 2) trie a pour clef la lettre que nous sommes en train de traiter. Si ce n’est pas le cas, alors nous ne faisons rien.

  Quant à edit_dist, cette variable nous permet de compter le nombre d’éditions que nous avons effectuées. Si nous effectuons une édition (comme nous le verrons ensuite), nous retirons 1 à edit_dist, ainsi, lorsque nous atteindrons 0 nous saurons qu’il n’est plus possible d’effectuer d’édition. Ici, puisque nous n’avons apporté aucune édition, nous laissons edit_dist tel quel. Finalement, end est tout simplement la fin du mot qui est passée à la fonction pour être traitée (soit pour avancer normalement comme nous le faisons ici, ou pour lui apporter une édition).

• Passons aux lignes 6 et 7, si le mot est vide word == '' et que l’on est sur une feuille trie == {}, nous remontons dans l’arbre (flèches bleues des figures précédentes). Pour que cette remontée puisse se faire correctement, nous ajoutons une valeur à correction (la manière d’ajouter un élément à un set est d’utiliser la méthode update). Ce que nous ajoutons est un tuple de deux éléments : le premier élément de ce tuple est une chaine de caractères vide (qui servira de base pour la reconstruction du mot), et le second élément est un entier qui nous servira à compter le nombre d’éditions qui ont été appliquées. Cette valeur nous permettra de trier la liste de suggestions de corrections en la triant des mots ayant la distance d’édition la plus faible aux mots ayant la distance d’édition la plus grande.

• Terminons avec la ligne 4. Pour rappel, map permet d’appliquer la fonction passée en premier argument à chacun des éléments de la liste qui est indiquée en second argument (no_editions). Le retour de ce map est ensuite ajouté à correction.

  Détaillons la partie lambda t: (letter + t[0], t[1]). Pour rappel, les lambdas sont ce que l’on appelle des fonctions anonymes… car elles n’ont pas de nom ! La ligne précédente est équivalente à ce code :

1
2

def fonction(t)
    return (letter + t[0], t[1])

Celle-ci prend donc un argument, nommé t. En réalité, t est un tuple de deux éléments, qui sont ceux que nous avons présentés à la ligne 7 : le premier est une chaine de caractère qui sert à reconstruire le mot en remontant dans l’arbre, et le deuxième est un entier qui stocke le nombre d’éditions. La syntaxe est un peu complexe et nous sommes obligés de passé par des indices pour accéder aux éléments du tuple, là où en Python 2 il était autorisé de faire du tuple unpacking dans les lambdas : lambda s, e: (letter + s, e) qui est plus lisible…

Nous voyons que nous ajoutons la lettre du nœud sur laquelle nous sommes à la chaine retournée (qui correspond à t[0]). Cela nous permet donc de reconstruire le mot à l’envers (comme dans les flèches bleues des figures). Pour « avocat », on part de la fin du mot avec "" auquel on ajoute les lettres du mot en remontant : "" → "" → "t" → "at" → "cat" → "ocat" → "vocat" → "avocat". Quant à t[1] la valeur reste inchangée car nous n’avons pas appliqué ici d’édition, nous nous sommes contentés d’avancer dans le mot.

Nous avons donc terminé la partie sans éditions. N’hésitez pas à relire cette partie pour bien la comprendre, puisque ce code nous servira de base par la suite pour appliquer les éditions, notamment les map et lambda. N’hésitez donc pas à jouer avec le code pour bien le comprendre

Avancer dans l’arbre : avec éditions

Nous allons donc passer à l’étape cruciale : l’ajout d’éditions, et nous allons commencer par gérer les délétions ou substitutions de lettres, puis nous traiterons les insertions et les transpositions. Le code sera relativement proche de celui que nous venons de voir.

Délétions et Subsitutions

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

if edit_dist > 0:
    # Déletions et Subsitutions
    for letter in trie:
        # deletion (l'utilisateur a oublié de taper une lettre)
        # -> on cherche la lettre manquante en s'autorisant à visiter tous les noeuds fils du noeud courant)
        deletion = _find_closest(trie[letter], edit_dist - 1, word)
        deletion = map(lambda t: (letter + t[0], t[1] + 1), deletion)
        corrections.update(deletion)

        # substitution (l'utilisateur a utilisé une lettre à la place d'un autre
        # -> on cherche la lettre correcte en s'autorisant à visiter tous les noeuds fils du noeud courant)
        if word[0:1] != letter:
            substitution = _find_closest(trie[letter], edit_dist - 1, word[1:])
            substitution = map(lambda t: (letter + t[0], t[1] + 1), substitution)
            corrections.update(substitution)

Nous commençons par vérifier à la ligne 1 qu’il est encore possible de faire une édition. Si tel est le cas, alors edit_dist sera strictement supérieur à 0. Dans le cas contraire, c’est à dire, si nous ne pouvons plus faire d’édition, nous passons directement au code que nous avons décrit à la section précédente.

Comme nous l’avons dit précédemment (voir cette partie), pour corriger une délétion ou une substitution, nous nous autorisons à visiter tous les nœuds fils d’un nœud donné. C’est donc pour cela que nous faisons une boucle à la ligne 3 sur tous les fils (les lettres) du nœud sur lequel nous sommes. Une particularité cependant selon si l’on traite une délétion ou une substitution :

• Dans le cas d’une délétion, le but est de rajouter la lettre manquante. Ainsi, on ne touche pas à la chaine de caractères du mot que l’on traite : celle-ci reste intacte. C’est pourquoi dans ce cas, l’appel à _find_closest prend pour dernier argument word, auquel nous n’avons pas touché.

  Par exemple, si l’utilisateur a rentré la chaîne « avoat » et que nous sommes sur le nœud « o », la chaîne restante (word) est « at ». Grâce à la boucle, letter prendra forcément à un moment pour valeur « c ». Ainsi, il existera un appel de la fonction tel que celui-ci : _find_closest(trie['c'], edit_dist - 1, "at")

• Dans le cas d’une substitution, le but est de rétablir la lettre erronée. Cela implique donc de ne pas prendre en compte la première lettre de la chaine que nous traitons. C’est donc pour cela que le dernier argument de _find_closest est word[1:], c’est-à-dire la chaîne de caractères d’entrée dont la première lettre a été retirée.

  Par exemple, si utilisateur a rentré la chaîne « avovat » et que nous sommes sur le nœud « o », la chaîne restante (word) est « vat ». Grâce à la boucle, de nouveau, letter prendra forcément à un moment pour valeur « c ». Sauf que contrairement à la délétion, letter (« c » donc) devra remplacer la première lettre de la chaîne restante. C’est pourquoi donc nous n’utilisons pas word dans l’appel, mais word[1:] (« at »). Cela nous permet donc de rétablir la lettre correcte. A noter, nous avons ajouté une condition dans le cas d’une substitution, où nous n’exécutons le code que si letter est différent de word[0:1] (d’où la condition à ligne 12) puisque sinon il ne s’agirait pas d’une substitution et cela ferait doublon avec le code où l’on avance sans appliquer d’édition.

• Pour terminer, et dans les deux cas, _find_closest renvoie un set contenant (ou non, il peut être vide) la liste des corrections du mot passé en paramètre. Pour chacun des set de retour, nous appliquons la fonction map avec la même expression que nous avons vue précédemment lambda t: (letter + t[0], t[1] + 1). Nous rajoutons à chacune des chaînes de caractères de retour la lettre qui permet de corriger le mot à ce stade.

  Un ‘détail’ cependant, l’expression n’est pas tout à fait la même, vous remarquerez que le deuxième élément du tuple est modifié cette fois-ci ! En effet, si le set de retour n’est pas vide c’est que nous avons effectivement appliqué une délétion ou une substitution à ce stade qui permet de corriger le mot. Il faut ainsi penser à indiquer dans le tuple de retour que nous venons de faire une édition en ajoutant 1 à la valeur contenue dans t[0].

Vous vous demandez probablement pour quelles raisons le set de retour serait vide. Il peut être vide si les éditions que nous avons tenté d’appliquer ne mènent pas à une fin de mot. C’est par exemple le cas dans la figure présentée pour les délétions et substitutions pour la tentative de correction qui a mené sur la branche du mot « avoine ». A partir du moment où l’on ne peut plus ① appliquer d’édition (if edit_dist > 0 vaut False) ② avancer normalement (if letter in trie vaut False) et ③ nous ne sommes pas sur une feuille (if word == '' and trie == {} vaut False) alors quoi qu’il arrive nous renvoyons corrections qui sera resté à sa valeur d’initialisation corrections = set(), c’est à dire un ensemble vide (noté {} en bleu dans la figure). Vous noterez que je ne le fais plus figurer ensuite dans les valeurs de retour bleues, et c’est normal, car ajouter le contenu d’un ensemble vide à un ensemble non vide … donne l’ensemble non vide de départ (pour rappel, la méthode update fait l’ajout inplace, c’est à dire, directement dans l’ensemble sur lequel on l’applique) :

1
2
3
4
5
6
7
8
9
10
11

>>> a = set('a')
>>> b = set()
>>> a.update(b)
>>> a
>>> {'a'} 
>>> # On retrouve donc l'ensemble de départ 'a'
>>> b = set('b')
>>> a.update(b)
>>> a
>>> {'b', 'a'}
>>> # L'ensemble a un élément de plus !

Insertions et Transpositions

Terminons donc par corriger les insertions et transpositions. Si vous avez bien compris le code précédent, vous pouvez tenter d’écrire le code avant de lire cette partie. Code que voici :

1
2
3
4
5
6
7
8
9
10
11
12

letter = word[1:2]
if letter in trie:
    # insertion (l'utlisateur a ajouté une lettre en trop dans le mot)
    # -> on s'autorise à passer au noeud de la lettre à l'indice word[1] et on ne considère pas word[0]
    insertion = _find_closest(trie[letter], edit_dist - 1, word[2:])
    corrections.update(map(lambda t: (letter + t[0], t[1] + 1), insertion))

    # transposition
    # -> on inverse la lettre à l'indice 1 et à l'indice 0 (on ne le fait que si word[1] est une clef)
    transposition = _find_closest(trie[letter], edit_dist - 1, word[0:1] + word[2:])
    transposition = map(lambda t: (letter + t[0], t[1] + 1), transposition)
    corrections.update(transposition)

• On commence par récupérer la deuxième lettre de la chaîne de caractère à la ligne 1 : letter = word[1:2]. En effet, que l’on soit dans le cas de l’insertion ou de la transposition, le caractère qui nous intéresse pour avancer dans l’arbre est le second :

  • Si l’utilisateur a ajouté une lettre par exemple « p » dans « avopcat » et que nous sommes rendus au nœud « o », pour corriger l’insertion, nous ne considérons pas le premier caractère de la chaîne, en effet, nous allons essayer de sauter directement vers le second caractère pour ainsi ne pas considérer le caractère surnuméraire.

  • Si l’utilisateur a fait une transposition, encore une fois c’est le second caractère qui nous intéresse. En effet, si l’utilisateur a interverti « c » et « a » dans « avoact » et que nous sommes sur le nœud « o », nous vérifions si le nœud « o » a pour fils le nœud « c ». Si tel est le cas, nous tentons une transposition en inversant « c » et « a » dans la chaîne et allons sur le nœud « c » pour ensuite tenter d’aller sur le nœud « a ». Dans ce cas encore une fois, c’est bien le deuxième caractère de la chaîne qui nous intéresse.
    

• Aux lignes 5 et 6, nous traitons le cas de l’insertion. Comme mentionné précédemment, nous visitons directement le nœud représentant le deuxième caractère (stocké dans letter) : _find_closest(trie[letter], edit_dist - 1, word[2:]). Cette fois-ci, nous ne passons pas la chaîne word intouchée, nous passons la suite de la chaine de caractère à partir du troisième caractère. Ainsi, si je reprends l’exemple « avopcat », nous sautons le « p » et accédons directement au nœud « c », ainsi la suite de la chaîne de caractère à passer pour la suite est donc bien « at » qui commence donc au troisième caractère de la chaine (« p » : 0, « c » : 1, et « a » à l’indice 2 donc en 3e position).

  Comme dans les autres cas, nous mettons à jour la valeur de edit_dist pour signaler que nous avons appliqué une édition. Et comme dans les exemples précédents, lors du retour, nous rétablissons la lettre correcte qui est ici letter. La lettre surnuméraire ne sera pas ajoutée lors du retour car à aucun moment nous n’allons visiter son nœud. En effet, dans ce cas-ci nous passons directement au deuxième caractère de la chaîne, ainsi, c’est comme si le premier caractère n’avait jamais existé et il ne sera donc pas rajouté au retour.

• Les lignes 10 et 11 permettent de traiter le cas de la transposition. Le processus est relativement similaire au cas de l’insertion, sauf sur la chaîne qui est passée par la suite. Ainsi, la chaîne passée à la fonction est recomposée ainsi word[0:1] + word[2:] où nous collons le premier caractère de la chaîne (word[0:1]) au reste de la chaîne à partir du troisième caractère (word[2:]), le deuxième caractère étant celui qui est actuellement traité (letter = word[1:2]).

  Par exemple, prenons la chaîne « avoact » et imaginons que nous sommes sur « o », ce qu’il reste à traiter est donc « act ». Le caractère que nous allons actuellement traiter (letter) est « c ». Ainsi, la suite de la chaîne de caractères à passer est word[0] (« a ») suivi de word[2:] (« t »), ce qui donne donc « at ». Ainsi, nous remettons les lettres dans le bon ordre, ce qui nous permet de rétablir l’orthographe correcte du mot lors du retour !

Nous avons donc terminé la méthode _find_closest qui est donc au cœur de l’application de correction. Le code n’est pas particulièrement compliqué une fois que l’on a compris comment utiliser l’arbre pour générer les éditions. N’hésitez pas à reprendre les diagrammes pour comprendre l’intuition sur la génération d’édition, et si le code vous pose problème, essayez de voir comment une partie du diagramme se traduit en code (par exemple, les flèches rouges, ou à quel moment les flèches bleues sont gérées dans le code).

Pour aller plus loin

Notre programme de correction fonctionne, mais nous pourrions y apporter quelques améliorations :

• Dans l’état actuel des choses, chaque édition à un coût fixe (de 1 : edit_dist - 1). Nous pourrions également imaginer pénaliser différemment chaque type d’édition. Les valeurs de pénalité devraient dans ce cas être calculées sur un corpus en regardant quelles erreurs sont les plus fréquentes. Si par exemple on se rend compte que la plupart des erreurs viennent d’une substitution ou d’une transposition, on pénaliserait moins ces éditions-ci que les autres.
• Dans le même ordre d’idée, on pourrait imaginer pénaliser différemment les éditions en fonction de la lettre touchée, comme le suggère Norvig. Ainsi, si l’on se rend compte que la plupart des erreurs proviennent d’un problème de doublement de lettre, on pénaliserait moins l’édition si elle consiste à doubler la lettre précédente pour rétablir l’orthographe correcte. J’imagine que c’est un cas d’erreur assez fréquent en français où les doubles lettres sont nombreuses (assurément, évidemment, occurrence, etc.).
• Nous présentons actuellement les propositions de correction du nombre d’éditions le plus faible au nombre d’éditions le plus haut. Cependant, dans une application réelle (un traitement de texte par exemple) nous devrions prendre en compte le contexte. Ainsi, l’on ne trierait pas seulement les mots en fonction du nombre d’éditions, mais également en fonction de la probabilité qu’ils ont d’apparaître avec le mot précédent (cela s’appelle un modèle de langue). Cela permettrait de fournir de meilleures suggestions de corrections à l’utilisateur.

Conclusion

Nous avons donc créé un programme de correction orthographique en utilisant des arbres n-aire, qui, comme nous l’avons vu, sont très pratiques et nous permettent de générer les éditions au bon moment.

Le programme complet est téléchargeable ici et est distribué sous licence Creative Commons 4.0 BY.