Arbres n-aires : Auto-complétion
Application des arbres n-aires à la création d'un programme d'auto-complétion simple en Python
Introduction
L’auto-complétion (ou autocomplete en anglais) désigne une fonctionnalité qui permet de suggérer à l’utilisateur un mot (ou groupe de mots) dès qu’il commence à saisir quelques caractères sur son clavier ; ceci afin de lui épargner de saisir l’ensemble du mot par lui-même. De tels programmes se trouvent notamment dans les outils classiques de traitement de texte (Word, LibreOffice, etc.) ou bien encore dans nos navigateurs (suggestions de recherche Google, Bing), nos téléphones ou bien encore, pour les plus programmeurs d’entre nous, dans la plupart des IDE modernes. Nous allons ici réaliser un programme d’auto-complétion simple en utilisant notamment un arbre n-aire qui permettra de stocker l’ensemble des mots du vocabulaire et nous permettra de proposer rapidement une suggestion à l’utilisateur.
Pour réaliser ce programme, nous aurons besoin d’un lexique. Je vous propose donc d’utiliser le lexique fourni par lexique.org, qui a l’avantage d’être assez complet et gratuit (j’utiliserai ici la version 3.83, mais toute autre version fait aussi bien l’affaire). Vous êtes bien sûr libre d’utiliser un autre lexique (en français ou non) si vous le souhaitez.
Approche Naïve
Avant de comprendre l’intérêt d’utiliser des arbres, et plus particulièrement des arbres n-aire, nous allons essayer de voir ce que donnerait une implémentation naïve. Ne voyez aucun jugement de valeur dans l’utilisation du terme naïf, qui ici désigne simplement une implémentation non optimisée et qui est souvent la plus évidente. On va voir ici que l’implémentation naïve, même si elle fonctionne en principe, n’est pas optimale.
Nous souhaitons donc que lorsqu’un utilisateur commence à taper un mot, le programme lui suggère une liste de mots commençant par les caractères rentrés par l’utilisateur. La solution à laquelle nous pouvons penser serait :
-
de charger tous les mots du dictionnaire dans une liste ;
-
d’attendre que l’utilisateur rentre une suite de caractères ;
-
de filtrer les mots de la liste en ne gardant que ceux qui commencent par les caractères rentrés par l’utilisateur.
De cette solution naïve, on peut mettre en avant deux problèmes en particulier :
- Pour la recherche des suggestions tout d’abord, la complexité en temps en élevée : elle est en O(n). Imaginons le pire cas dans lequel nous puissions nous trouver : les mots de la liste sont dans un ordre aléatoire et nous recherchons un mot commençant par « choc ». Pour retrouver l’ensemble des mots qui commencent par « choc », il est nécessaire de parcourir l’ensemble de la liste. En effet, puisque les mots de la liste sont dans un ordre aléatoire, des mots commençant par « choc » peuvent se retrouver aussi bien au début qu’à la fin de la liste, il est donc nécessaire de la parcourir en entier. Même si dans notre liste il n’y avait aucun mot qui ne commençait par « choc », nous n’aurions pas le choix et serions obligés de passer en revue tous les mots de la liste pour nous en assurer. Ainsi, si la liste contient n mots, il faudra donc passer en revue chacun des n éléments, la complexité de l’opération est donc bien en O(n) ;
- Intuitivement, nous sentons bien que la liste n’est pas une structure de données optimale. En effet, dans une liste de mots, beaucoup commencent par un préfixe commun [‘abricot’, ‘avocat’, ‘avoine’, …, ‘choc’, ‘chocolat’, ‘chocolaté’, …] et une simple liste ne nous permet pas de tirer parti de cela. Or, pour un programme d’autosuggestion, c’est exactement d’une structure de données qui tirerait parti de ce fait dont nous aurions besoin. Ainsi, si l’on remarque que le préfixe du mot n’a rien à voir avec l’entrée fournie par l’utilisateur, nous aimerions passer directement à des mots dont le préfixe serait celui recherché.
Nous allons donc utiliser ici une structure de données spécifique qui permet de régler les problèmes que nous venons d’évoquer. Notamment, la solution proposée permettra de rechercher des suggestions intelligemment ; en effet, dans l’approche naïve, nous devons comparer le début de tous les mots de la liste à l’entrée donnée par l’utilisateur. C’est relativement peu efficace, on l’a dit, mais on ne peut faire autrement dans ce cas. L’approche proposée, qui utilise des arbres n-aire nous permettra de solutionner se problème en nous évitant d’avoir à comparer l’entrée de l’utilisateur à tous les mots du dictionnaire.
Les arbres
Un peu de terminologie
Tout d’abord, qu’est qu’un arbre ? Un arbre est une structure de données arborescente. Un arbre comporte un certain nombre de nœuds (ici représentés par des cercles). Dans un arbre enraciné (également appelé une arborescence), comme c’est le cas ici, il y a un nœud particulier, le nœud racine qui est le nœud qui constitue le point d’entrée de l’arbre et qui est hiérarchiquement le nœud le plus élevé.
Deux nœuds sont reliés entre eux par un certain nombre de branches — dans la figure ci-dessous chaque nœud a au plus deux branches, c’est donc un arbre binaire — qui permet à chaque nœud d’être relié au plus à deux nœuds fils. Il peut cependant n’avoir qu’un seul ou même zéro fils. Un nœud qui a au moins un fils est un nœud interne (par exemple B, C ou D), tandis qu’un nœud qui n’a pas de fils est appelé une feuille (ou nœud externe, comme J, G ou bien K). Tous les nœuds ont un nœud père (p.ex. D est le nœud père de G) à l’exception du nœud racine, qui par définition n’est le fils d’aucun nœud. Chaque nœud contient une certaine valeur, ici représentée par une étiquette.
Comme vous pouvez le remarquer, un arbre à une structure récursive. Ainsi le fils du nœud B — c’est-à-dire le nœud D — peut être considéré comme la racine d’un arbre plus petit qui comporterait les nœuds F, G et J. Ainsi, la zone en rouge constitue le sous-arbre (gauche) du nœud B (B n’ayant pas de fils droit, il n’a qu’un seul sous-arbre).
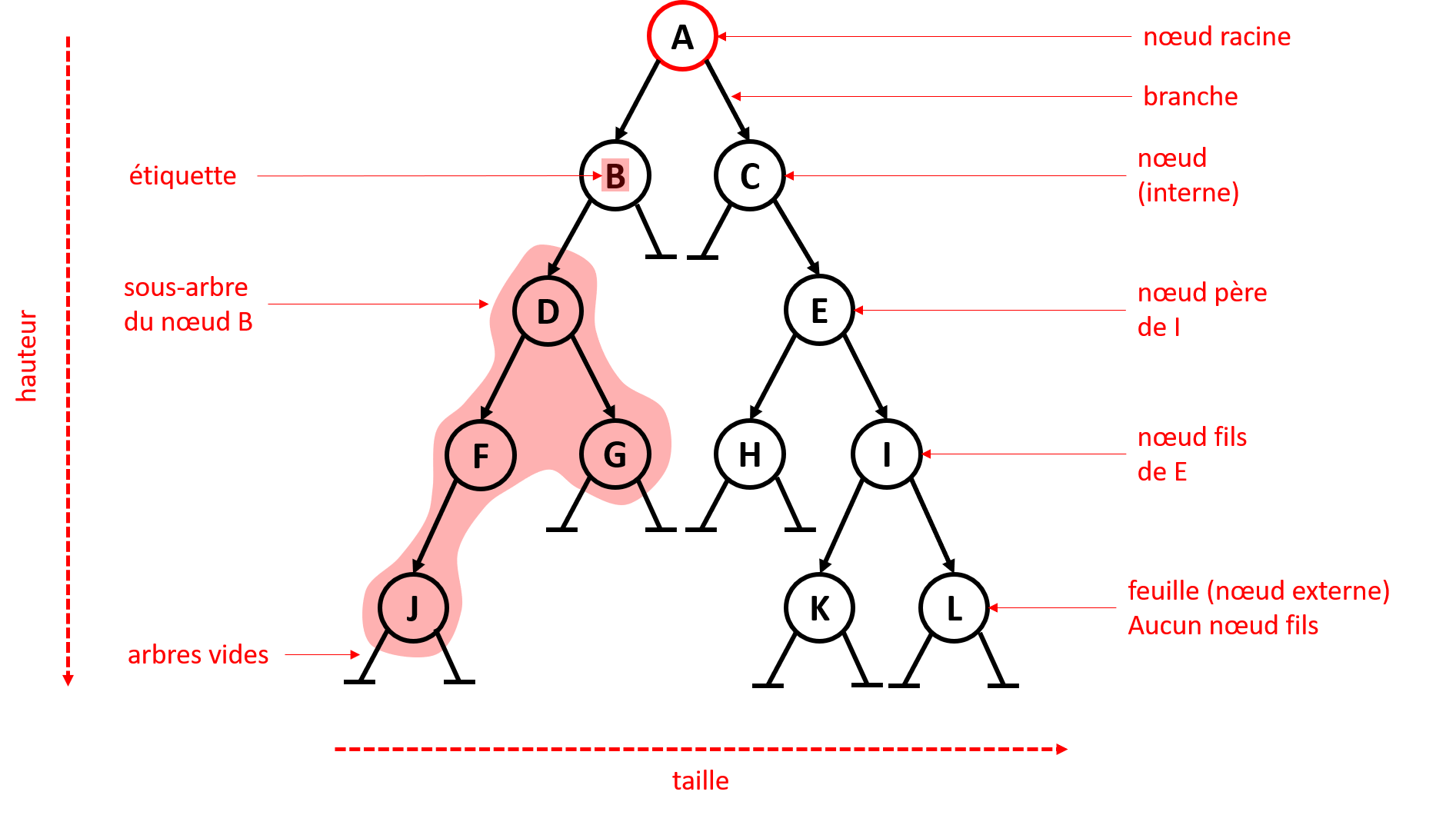
Le degré d’un arbre indique le nombre maximum de fils qu’un nœud peut accueillir. Ainsi, un arbre unaire est un arbre de degré 1 où chaque nœud ne peut avoir qu’au plus un seul fils (il s’agit en réalité d’une liste chaînée), un arbre binaire est un arbre de degré 2 ou chaque nœud ne peut avoir qu’au plus 2 fils, …, un arbre n-aire est un arbre ou chaque nœud ne peut avoir qu’au plus n nœud fils.
Un arbre pour stocker des mots
Nous allons donc nous servir d’un arbre pour stocker l’ensemble des mots du dictionnaire. Et plus particulièrement, nous allons nous servir d’un arbre n-aire pour les stocker. Ainsi, chaque nœud aura au plus n nœud fils. Plus précisément, nous allons utiliser une structure de données qui s’appelle un trie (de l’anglais retrieval) qui est, comme son nom l’indique, optimisé pour la recherche. En français, ce type d’arbre est appelé arbre préfixe. On peut graphiquement représenter un arbre n-aire comme dans la figure ci-dessous qui contient les mots suivants : « abricots », « avocat », « avoine », « ananas », « banane », « baie », « kiwi » et « kiwis » :
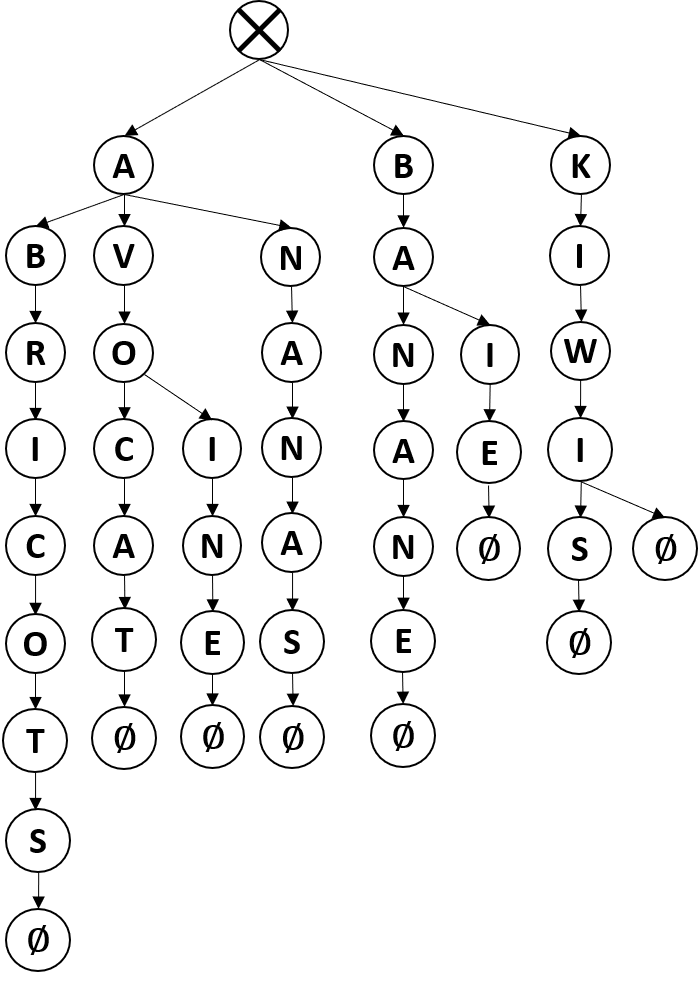
Le nœud racine est ici représenté par le nœud barré et a ici 3 nœuds fils « a », « b » et « k ». On voit que dans un tel arbre, les mots sont stockés lettre par lettre, où chaque lettre d’un mot donné est représentée par un nœud. Un nœud donné a pour nœud fils la lettre qui suit dans le mot considéré. Ainsi, si l’on parcourt, depuis le nœud racine, les nœuds situés les plus à droite, on rencontre d’abord, « k », puis « i », puis « w » puis « i », et pour finir « ∅ » ; formant ainsi le mot « kiwi∅ ». Là où le nœud racine marque le début de l’ensemble des mots stockés dans l’arbre, la fin des mots est représentée par le symbole « ∅ » (en réalité peu importe le symbole, pourvu qu’il y ait un symbole qui représente les fins de mots) ; ainsi le mot codé est « kiwi ».
Il est indispensable d’utiliser le caractère de fin de mot « ∅ », car il permet de savoir où se terminent les mots. En effet, sans un tel caractère, n’importe quelle suite de nœuds pourrait théoriquement constituer un mot (« abr », « anan »). On peut remarquer que cet arbre contient les mots « kiwi » et « kiwis » (le caractère ∅ suit le « i » et un autre suit le « s ») ; mais cet arbre ne contient pas le « abricot ». En effet, le caractère de fin de mot ∅ est situé après le « s » et aucun ne suit le « t ». Si l’on souhaitait que « abricot » constitue un mot, il suffirait de rajouter le caractère de fin mot à la suite du « t ».
Quel intérêt ?
En quoi utiliser un arbre n-aire nous permet-il de solutionner les problèmes que l’on a soulevés avec l’approche naïve ? On remarque que les préfixes communs à différents mots sont mutualisés. Par exemple, « baie » et « banane » qui partagent tous deux le préfixe « ba » partagent également les nœuds « b » et « a ». On voit que depuis l’unique nœud « a » on peut atteindre les nœuds représentant la fin des mots « banane » et « baie ». Cette structure de données permet donc de faire exactement ce que nous souhaitons, c’est-à-dire retrouver l’ensemble des mots qui commencent par un préfixe donné.
Maintenant, comment faire pour retrouver tous les mots qui commencent par un préfixe donné, disons « avo » ? En partant du nœud racine, on va égrener le préfixe fournit par l’utilisateur lettre à lettre pour essayer d’avancer d’un nœud à l’autre dans l’arbre. Ainsi, dans le cas où le préfixe est « avo » il suffit de partir du nœud racine, d’aller sur le nœud représentant le « a », puis le « v », puis le « o ». Une fois arrivé sur la dernière lettre du préfixe, il va suffire de parcourir chacun de ses fils pour reconstituer les mots !
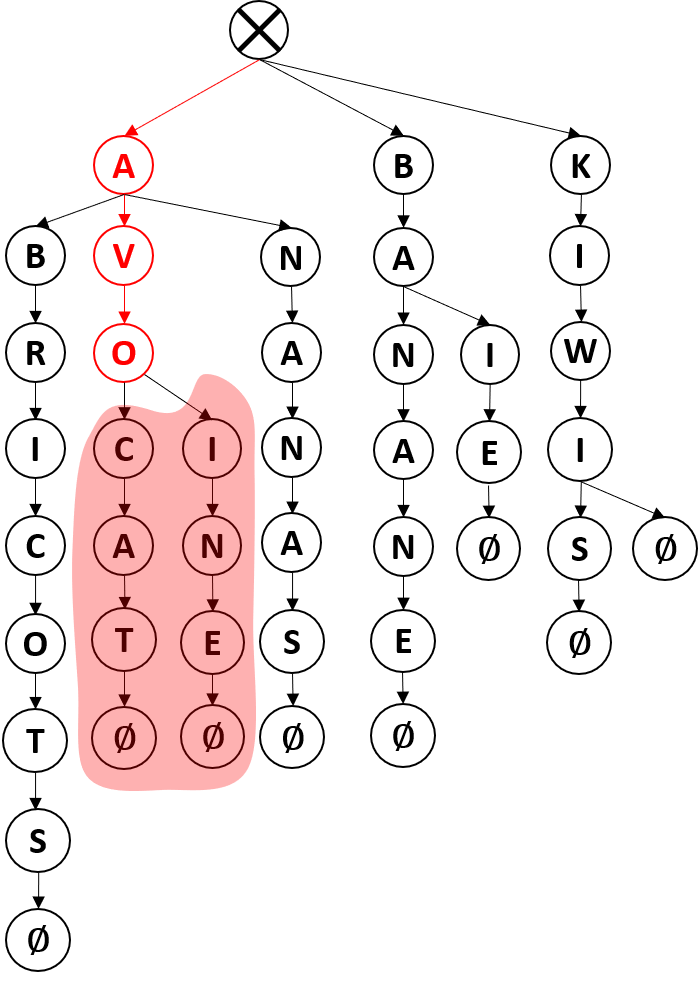
Ainsi, utiliser un arbre résout notre problème :
- Chercher si un préfixe existe ou non dans l’arbre ne dépend plus du nombre de mots dans l’arbre, mais seulement du nombre de lettres du préfixe. Si le préfixe existe, on fait autant d’opérations qu’il y a de lettres dans le préfixe, on est donc en O(m) où m représente le nombre de lettres du préfixe. Si le préfixe n’existe pas dans l’arbre, dans ce cas, on arrête de parcourir l’arbre dès que l’on ne peut plus avancer d’un nœud. Ainsi, si l’on cherchait le préfixe « foo » dans l’arbre, nous ne pourrions aller plus loin que le nœud racine, car celui-ci n’a aucun nœud représentant le « f ». Plus besoin donc de regarder l’ensemble des mots un à un puis de regarder si leur préfixe correspond au préfixe recherché, on ne parcourt que le sous-arbre du préfixe qui nous intéresse.
- Les mots sont naturellement regroupés par préfixe, et les préfixes sont mutualisés entre tous les mots qui les partagent.
Code
Pour ne pas perdre de temps et pour se focaliser sur le point clef de l’article, je vous fournis le code de l’interface (interface.py) et le main (main.py), et nous construirons la classe Trie (dans trie.py) ensemble. Le code complet de l’application est téléchargeable dans la Conclusion.
Un arbre avec un dict()
Il y a plusieurs façons d’implémenter un arbre n-aire, par exemple en utilisant un classe Trie et une classe Noeud avec un attribut permettant de contenir la liste de ses enfants (ce qui est d’ailleurs le moyen de faire classique en C, à l’exception que l’on utiliserait une structure et non une classe, et un tableau plutôt qu’une liste).
Je vous propose ici d’implémenter un arbre n-aire en utilisant simplement des dictionnaires Python classiques. Ainsi, l’arbre montré dans les figures précédentes peut être avantageusement et simplement représenté par un dictionnaire ainsi :
1
2
3
4
5
6
7
8
{'a': {'b': {'r': {'i': {'c': {'o': {'t': {'s': {'∅': {}}}}}}}},
'n': {'a': {'n': {'a': {'s': {'∅': {}}}}}},
'v': {'o': {'c': {'a': {'t': {'∅': {}}}},
'i': {'n': {'e': {'∅': {}}}}}}},
'b': {'a': {'i': {'e': {'∅': {}}},
'n': {'a': {'n': {'e': {'∅': {}}}}}}},
'k': {'i': {'w': {'i': {'∅': {},
's': {'∅': {}}}}}}}
Dans notre implémentation un nœud est représenté par un dictionnaire. L’étiquette de ses nœuds fils sont les clefs de ce dictionnaire. La valeur associée à ces clefs est un dictionnaire qui contient les enfants de ce nœud fils (ainsi, un nœud ‘complet’ est représenté par son étiquette — la clef du dictionnaire — et la liste de ses enfants par un dictionnaire — la valeur associée à la clef). Ainsi, un arbre est un ensemble de dictionnaires imbriqués les uns dans les autres. Le dictionnaire peut éventuellement être vide, dans ce cas, cela signifie que le nœud qu’il représente n’a pas d’enfants. C’est par exemple le cas du caractère de fin de mot ∅ qui ne peut naturellement pas avoir d’enfants, puisque aucune lettre ne peut apparaître après la fin d’un mot … sinon ça n’en serait pas la fin.
Nous commençons donc simplement par créer une class Trie.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Trie:
def __init__(self, end='∅', words=[]):
"""
Initialisation de l'objet
(rappel en Python, le constructeur est __new__, __init__ n'est qu'un instantiateur)
:param end: signe de fin de mot à utiliser
:param words: liste des mots à ajouter au trie
"""
self.root = {}
self.end = end
if words:
self.add_words(words)
J’ai mis comme paramètre de l’instantiateur le caractère de fin de mot à utiliser end (ici '∅', mais une chaîne vide marcherait tout aussi bien), ainsi que words qui permet de passer la liste des mots à insérer dans le Trie. Tous deux sont des paramètres optionnels.
La classe a donc deux attributs :
-
rootqui est donc le nœud racine. Comme mentionné précédemment, celui-ci est représenté par un dictionnaire ; dictionnaire qui est vide à l’initialisation, l’arbre ne contenant aucun mot. -
endqui stockera le caractère de fin de mot
A la ligne 11, nous vérifions si la liste de mots n’est pas vide (pour rappel [] est évalué à False). Si c’est bien le cas, nous faisons appel à la méthode add_words que nous allons créer maintenant et qui nous permettra d’ajouter l’ensemble des mots contenus dans la liste words au trie.
Ajouter des mots
Pour ajouter des mots à notre arbre, je vous propose d’ajouter deux méthodes : une méthode add_words qui prendra comme argument une liste de chaînes de caractères, et une méthode add_word (qui sera notamment appelée par add_words) et qui prendra comme argument une chaîne de caractères.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def add_words(self, words):
"""
Permet d'ajouter DES mots au Trie
:param words: liste de chaines de caractères
:return: void
"""
for word in words:
self.add_word(word)
def add_word(self, word):
"""
Permet d'ajouter UN mot au Trie
:param word: chaine de caractères
:return: void
"""
trie = self.root
for letter in word:
trie = trie.setdefault(letter, {})
trie[self.end] = {}
Détaillons un peu ce qu’il se passe dans la méthode add_word qui est un peu technique :
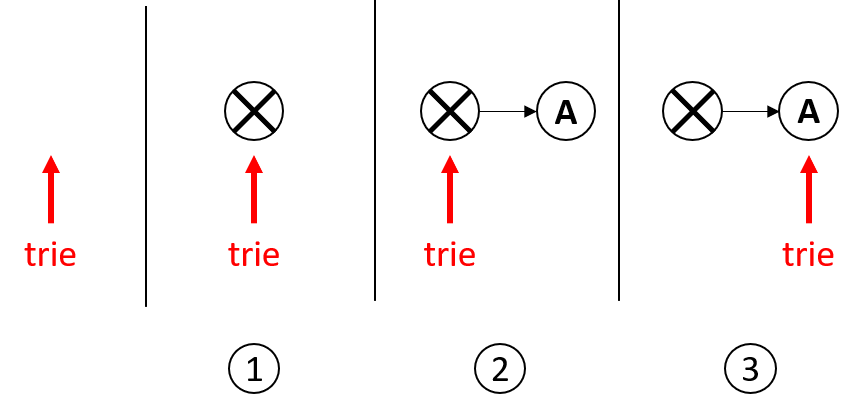
-
On commence tout d’abord par récupérer le nœud racine que l’on stocke dans une variable :
trie = self.root(étape ①) -
Pour chacune des lettres du préfixe entré par l’utilisateur (
for letter in word) on va soit se déplacer sur le nœud qui correspond à la lettreletteren cours si ce nœud existe (dans ce cas, on va directement à l’étape ③), sinon on va créer ce nœud (étape ②) et se placer dessus (étape ③). Cette opération peut être avantageusement réalisée au moyen de la méthodesetdefault. Formellement, la code de la ligne 19 est équivalent à celui-ci :
1
2
3
4
5
6
7
8
9
10
if letter in trie:
# Le noeud sur lequel l'on est a un noeud fils correspondant à la lettre en cours
# On se place donc sur ce noeud
trie = trie[letter]
else:
# Sinon, le noeud sur lequel l'on est n'a pas de noeud fils correspond à la lettre en cours
# On ajoute une nouvelle clef (= un nouveau noeud) au noeud sur lequel on se trouve
trie[letter] = {}
# Puis on se place sur le noeud nouvellement ajouté
trie = trie[letter]
- La dernière étape (l. 21) intervient une fois le mot entièrement rentré dans le Trie, où il ne reste plus qu’à ajouter le caractère de fin de mot au nœud courant (qui est nécessairement la dernière lettre du mot).
Pour mieux comprendre ce qu’il se passe, je vous invite à faire en sorte que votre programme produise une trace. Vous pouvez ce faire en ajoutant des print dans la version du code ci-dessus.
Afficher/Cacher le contenu masqué
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def add_word(self, word):
"""
Permet d'ajouter UN mot au Trie
:param word: chaine de caractères
:return: void
"""
trie = self.root
previous_node = 'ROOT'
for letter in word:
print('\nContenu du noeud {}'.format(previous_node))
pprint(trie)
if letter in trie:
print('Le noeud "{}" fils du noeud "{}" EXISTE.\n'\
'On se place sur le noeud "{}".'.format(letter, previous_node, letter))
trie = trie[letter]
previous_node = letter
else:
print('Le noeud "{}" fils du noeud "{}" N\'existe PAS: '\
'création du noeud.'.format(letter, previous_node))
trie[letter] = {}
print('On se place sur le noeud "{}".'.format(letter))
trie = trie[letter]
previous_node = letter
print('Création du noeud "{}", fils du noeud "{}"'.format(self.end, letter))
trie[self.end] = {}
print('Le mot {} a été rentré dans l\'arbre'.format(word))
print('-'*25)
Compter le nombre de nœuds et le nombre de mots
Avant de rentrer dans le vif du sujet, à savoir, proposer des suggestions à l’utilisateur, je vous propose d’écrire deux méthodes. La première, num_words, permettra de compter le nombre de mots présents dans l’arbre, et la seconde, num_nodes permettra de compter le nombre de nœuds dans l’arbre. Cela nous permettra de nous exercer à parcourir l’arbre, et nous le ferons au moyen de méthodes récursives.
Compter les mots
Nous allons donc commencer par créer une méthode pour compter le nombre de mots dans l’arbre. Avant de se jeter dans le code, réfléchissons : comment savons-nous où un mot s’arrête ? Nous avons défini que la fin d’un mot serait systématiquement marquée par un nœud particulier dont l’étiquette serait un caractère défini à la l’avance (dans notre cas ∅ stocké dans l’attribut end). Ainsi, il suffit de compter le nombre de nœuds ayant cette étiquette dans l’arbre, et nous aurons le nombre de mots !
Pour compter le nombre de mots, il va donc falloir parcourir toutes les branches de l’arbre. Nous allons nous servir d’une propriété que nous avons notée plus haut, la structure récursive de notre structure de données. Ainsi, le fils d’un nœud particulier peut être considéré comme la racine d’un sous-arbre plus petit. Ainsi, pour explorer complètement un arbre, il suffit d’explorer chacun de ses fils (qui constituent chacun un sous-arbre), ce qui consiste à explorer chacun des fils des fils, etc.
1
2
3
4
5
6
7
8
def num_words(self, trie=None):
trie = self.root if trie == None else trie
n = self.end in trie
for letter in trie:
n += self.num_words(trie[letter])
return int(n)
Analysons ce code :
- A la ligne 2 nous nous plaçons sur le nœud passé en paramètre. Si aucun nœud n’est passé en paramètre, nous nous plaçons sur le nœud racine
self.root. - A la ligne 4, nous déclarons une variable
net plaçons dans la variable la valeur retournée parself.end in trie. Ce que nous faisons ici, c’est que nous regardons si le nœud sur lequel nous nous trouvons (nœud qui est stocké dans la variabletrie) a un fils qui aurait pour étiquette « ∅ » (self.end). Si c’est le cas, alorsself.end in trievautTruequi est évalué à1par Python (par exemple si nous sommes sur le « i » de « kiwi »). Dans le cas, contraire,self.end in trievautFalsequi est évalué à0par Python (par exemple, si nous sommes sur le « w » de « kiwi », car « w » n’a qu’un seul fils — « i » — qui n’est pas le caractère de fin de mot). Si cette façon de faire ne vous paraît pas très intuitive, vous pouvez la remplacer par celle-ci qui est plus intuitive lorsque l’on débute :
1
2
3
4
if self.end in trie:
n = 1
else:
n = 0
- A la ligne 5, nous allons parcourir chacun des fils du nœud sur lequel nous nous trouvons, qui, pour rappel, aura pour étiquette
letter - A la ligne 6, nous réalisons un appel récursif (la méthode s’appelle elle-même). Cette fois-ci, nous lui donnons un paramètre : l’arbre qu’il faut explorer ensuite. Pour ce faire rien de plus simple, nous passons le dictionnaire lié à l’étiquette qui nous intéresse
trie[letter]. Et la fonction sera appelée autant de fois que le nœud sur lequel nous sommes a de fils, de même pour les fils de chacun des fils, etc. Si un nœud n’a pas de fils, alors il n’y aura rien à explorer et nous arrêterons donc de faire un appel récursif (puis que nous ne rentrerons même pas dans la boucle de la ligne 5) - Pour finir, nous ajoutons ce que la méthode nous renverra à la variable
n; variable que nous retournons à la ligne 8.
Ici, nous sommes assurés que la fonction récursive s’arrêtera puisque celle-ci est appelée pour chaque fils d’un nœud donné. Etant donné qu’un nœud n’a qu’un nombre fini de fils, nous sortirons forcément de la boucle de la ligne 5.
Maintenant que nous avons cette méthode, nous allons en profiter pour faire une assertion dans l’instantiateur et vérifier que l’arbre contient bien autant de mots que le nombre de mots qu’il y avait à ajouter.
1
2
# Code à rajouter à la suite de la ligne 14 de l'instantiateur
assert len(set(words)) == self.num_words(), "Problème à la construction du Trie : mots manquants !"
Ce code nous permet de nous assurer que l’arbre contient bien autant de mots qu’il y en a dans la liste passée en entrée (et si ce n’est pas le cas, nous signalons l’erreur à l’utilisateur et arrêtons le programme.)
Compter les noeuds
Compter le nombre de nœuds dans l’arbre revient à écrire un code quasiment identique à celui que nous venons d’écrire. La seule différence est ici à la ligne 4. Ici, nous initialisons directement n a 1. En effet, à partir du moment où cette fonction est appelée, c’est que nous sommes sur au moins un nœud. Même si l’arbre ne contient aucun mot, il y a au moins un nœud : le nœud racine.
1
2
3
4
5
6
7
8
def num_nodes(self, trie=None):
trie = self.root if trie == None else trie
n = 1
for letter in trie:
n += self.num_nodes(trie[letter])
return n
Suggérer des mots à l’utilisateur
Maintenant que nous avons ajouté des mots à l’arbre et que nous savons parcourir l’arbre de façon récursive, nous avons toutes les clefs en main pour suggérer des mots à l’utilisateur. Je vous propose donc de créer une méthode startswith qui prendra comme un argument un préfixe (une chaîne de caractères) et qui renverra l’ensemble des mots dans l’arbre qui commencent par le préfixe donné.
La méthode startswith
La première chose que nous allons faire dans la méthode startswith va consister à vérifier que le préfixe entré par l’utilisateur existe dans l’arbre. Si ce n’est pas le cas, nous renverrons une liste vide, dans le cas contraire, nous peuplerons cette liste avec l’ensemble des mots qui commencent par le préfixe donné. Voici le code de l’ensemble de la méthode startswith que nous allons détailler ci-après.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def startswith(self, prefix):
"""
Permet de retrouver tous les mots qui commencent avec le préfixe `prefix`
:param prefix: chaine de caractères
:return: set de chaines de caractères
"""
trie = self.root
suggestions = []
# Pour chacune des lettres du préfixe
for letter in prefix:
# On essaye d'avancer dans l'arbre
if letter in trie:
trie = trie[letter]
else:
# Si on n'y arrive pas, on retourne un set vide
return suggestions
# Si on est là, le préfixe existe bien dans l'arbre !
# Il ne reste plus qu'à parcourir chacune des branches et reconstruire l'ensemble des mots
suggestions.extend(map(lambda suffix: prefix+suffix, list(self._parcours(trie))))
# Et on retourne le tout
return suggestions
-
A la ligne 7, nous nous plaçons sur la racine de l’arbre, comme nous l’avons fait dans les codes précédents
-
A la ligne 8, nous déclarons une liste (pour l’instant vide) qui nous permettra de stocker l’ensemble des mots qui commencent par le préfixe spécifié par l’utilisateur
-
De la ligne 11 à ligne 17, nous vérifions que le préfixe rentré par l’utilisateur existe bel et bien dans l’arbre. Pour ce faire, nous parcourons l’arbre en regardant lettre à lettre le préfixe spécifié par l’utilisateur. A partir du moment où nous sommes bloqués sur un nœud (la lettre en cours ne n’est pas une étiquette d’un nœud fils du nœud sur lequel nous sommes), nous retournons la liste de suggestions, qui est restée vide. Sinon, nous avançons de nœud en nœud dans l’arbre.
-
La ligne 21 est la ligne qui nous permet de récupérer l’ensemble des suggestions pour le préfixe donné. Elle fait appel à la méthode
_paroursque nous allons détailler ensuite. Cette méthode prend comme argument un nœud, qui est le nœud qui correspond à la dernière lettre du préfixe. En effet, ce que nous souhaitons faire est explorer l’ensemble des nœuds fils de la dernière lettre afin de récupérer l’ensemble des fins de mots. Ainsi,list(self._parcours(trie))va contenir l’ensemble des suffixes possibles pour un préfixe donné. Ce qu’il nous reste à faire de recomposer les mots en ‘collant’ le préfixe fourni par l’utilisateur à chacun des suffixes qui auront été retrouvés. C’est ce que permet de faire la fonctionmap(cf. la documentation de Python). Et pour finir, nous ajoutons l’ensemble des mots reconstitués à la liste de suggestions, que nous renvoyons à la ligne 24.Pour information, et pour mieux comprendre la fonction
mapvous pouvez faire tourner ce code :
1
2
3
4
prefixe = "avo"
suggestions = list(map(lambda suffixe: prefixe+suffixe, ['ine', 'cat']))
print(suggestions)
['avoine', 'avocat']
Qui nous retourne bien ['avoine', 'avocat']. Ainsi, pour chaque suffixe (['ine', 'cat']) nous avons collé le préfixe 'avo' à chacun d’eux, ce qui nous a permis de former les mots précédemment cités. L’opération de collage a été effectuée par une expression lambda qui permet de faire des fonctions anonymes. Formellement, le code précédent est équivalent à celui-ci :
1
2
3
4
5
6
def coller(suffixe):
return prefixe + suffixe
prefixe = "avo"
suggestions = list(map(coller, ["ine", "cat"]))
print(suggestions)
Ainsi, l’expression lambda nous a permis “d’économiser du code” en nous évidant d’avoir à déclarer une fonction ad-hoc qui n’aurait été utile que dans ce cas.
La méthode _parcours
Il nous reste maintenant à écrire la méthode _parcours qui nous permettra de récupérer l’ensemble des suffixes d’un préfixe donné. Pour rappel, les méthodes préfixées du soulignement _ sont considérées comme des méthodes privées en Python. Tout comme les fonctions num_words et num_nodes, cette méthode sera récursive.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def _parcours(self, trie):
"""
Permet de parcourir le Trie récursivement
:param trie: Un dictionnaire représentant le noeud à explorer
:return: set de chaines de caractères
"""
suffix = []
# Est-on sur une feuille ?
if trie == {}:
return [""]
for letter in trie:
suffix.extend(map(lambda suffix: letter + suffix, list(self._parcours(trie[letter]))))
return suffix
Cette méthode prend en entrée le nœud duquel on souhaite obtenir le sous-arbre ; sous-arbre que nous appelons trie. Détaillons les points importants de ce code :
-
La ligne 10 est la ligne cruciale de ce code ! Nous regardons si le nœud sur lequel nous sommes est une feuille, auquel cas, c’est que nous serions arrivés au bout d’un mot. Si tel est le cas, nous renvoyons une liste contenant une chaîne vide
"". Celle-ci sera la base du mot que nous reconstruirons récursivement lettre par lettre. -
Les lignes 13 et 14 sont les lignes qui permettent d’explorer le reste de l’arbre de manière récursive. Notez que nous faisons appel à la méthode
_parcourspour chacun des nœuds fils sur lequel nous sommes. Contrairement au fonctionnum_nodesetnum_wordsoù nous faisions un simple appel récursif sans plus traiter les données de retour (mis à part une simple addition), ici les données de retour passent par la fonctionmap. Ce que nous faisons ici, c’est que nous ajoutons au début de la chaîne l’étiquette du nœud dont nous venons d’explorer les enfants.
Pour mieux comprendre comment les mots sont (re)construits de manière récursive, voici une figure illustrant le processus :
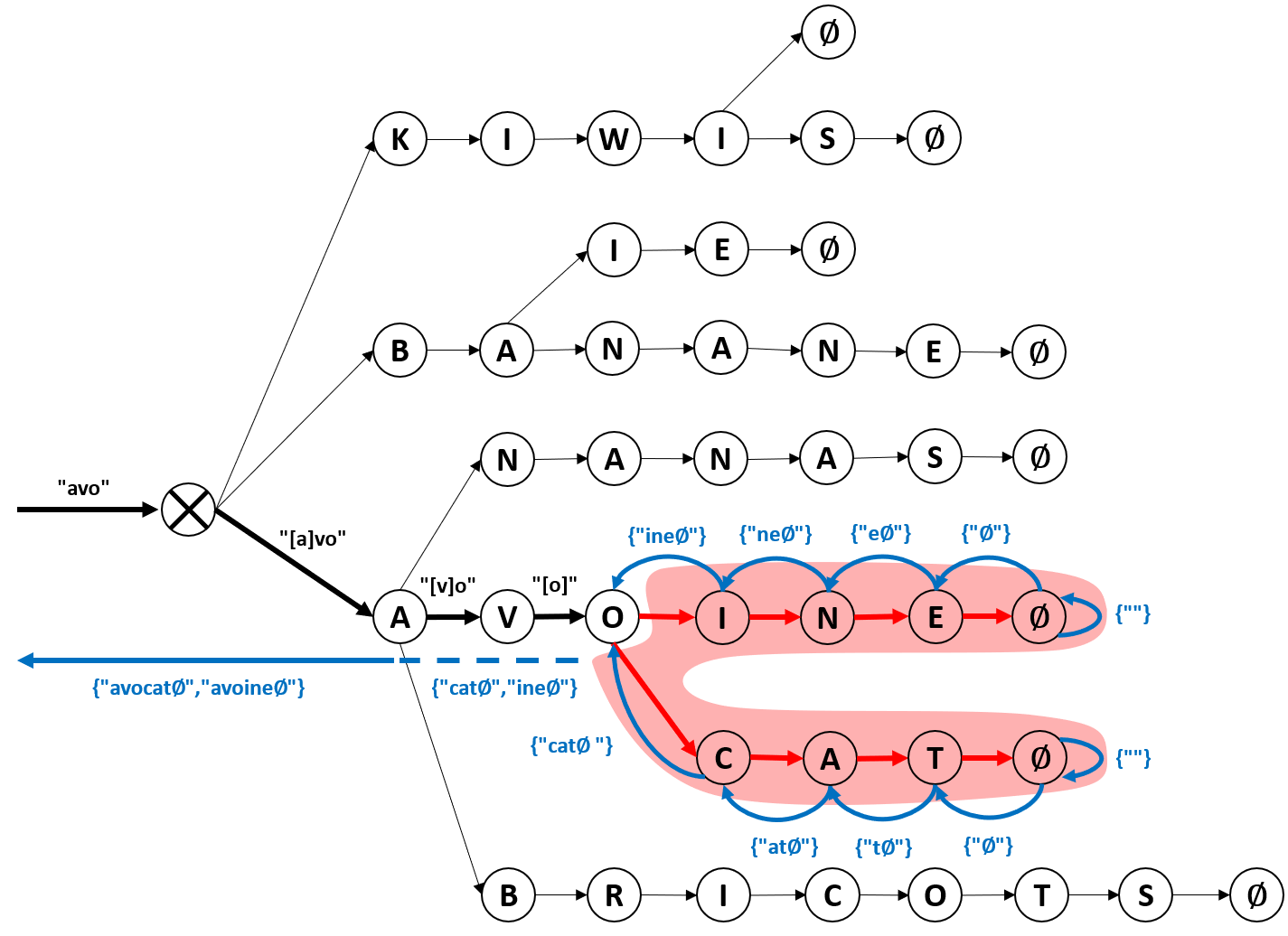
- Admettons que le préfixe fourni par l’utilisateur est « avo », nous parcourons tout d’abord l’arbre à partir de la racine et allons de nœud en nœud jusqu’au nœud représentant le « o », où sommes arrivés à la dernière lettre du préfixe (chemin en noir dans la figure, le code qui fait cela est dans la méthode
startswithde la ligne 11 à 17). - A partir de là, il faut récupérer les suffixes possibles à partir du nœud sur lequel nous sommes (ici indiqués en rouge, nous le faisons grâce à la méthode
_parcoursappelée parstartswithà la ligne 21). - La première chose que fait
_parcoursest de vérifier si le nœud que nous explorons est une feuille, ce qui voudrait dire, que par définition il n’aurait pas de fils, donctrie == {}. Si tel est le cas, nous renvoyons une liste contenant une chaîne vide qui sera la base du mot à reconstruire (ligne 11). Cette opération déclenche la « remontée » de la branche parcourue et est figurée en bleu. Lors de la remontée, nous allons ajouter l’étiquette du nœud dont nous venons d’explorer les fils à l’ensemble des chaînes de caractères retournées. Cela se fait au moyen de la fonctionmap. De nouveau nous utilisons une expression lambdalambda suffix: letter + suffixoùsuffixprendra alternativement pour valeur chacun des chaînes de caractères de la listelist(self._pacours(trie[letter])). - Si ne nous sommes pas sur une feuille, nous explorons chacun des fils du nœud sur lequel nous sommes (ligne 14 au moyen de l’appel récursif, symbolisé par des flèches rouges dans la figure :
self._parcours(trie[letter])). - Ainsi, à la ligne 21 de
startwith, la liste de retour obtenue contient deux éléments["cat", "ine"], pour lesquels nous n’avons plus qu’à préfixer le préfixe fourni par l’utilisateur, comme détaillé précédemment.
Voici une trace de la méthode parcours pour que vous puissiez comprendre son fonctionnement plus en détail.
Afficher/Cacher le contenu masqué
ALLER 0e appel de la méthode _parcours (exploration des fils du noeud o, 0/2 fils explorés) suffix=[] | ALLER 1e appel de la méthode _parcours (exploration des fils du noeud c, 0/1 fils explorés) suffix=[] | | ALLER 2e appel de la méthode _parcours (exploration des fils du noeud a, 0/1 fils explorés) suffix=[] | | | ALLER 3e appel de la méthode _parcours (exploration des fils du noeud t, 0/1 fils explorés) suffix=[] | | | | ALLER 4e appel de la méthode _parcours (exploration des fils du noeud ∅, 0/0 fils explorés) suffix=[] | | | | RETOUR Fin de mot ! | | | RETOUR 3e appel de la méthode _parcours (exploration des fils du noeud t, 1/1 fils explorés) lettre ajoutée : ∅ | suffix=['∅'] | | RETOUR 2e appel de la méthode _parcours (exploration des fils du noeud a, 1/1 fils explorés) lettre ajoutée : t | suffix=['t∅'] | RETOUR 1e appel de la méthode _parcours (exploration des fils du noeud c, 1/1 fils explorés) lettre ajoutée : a | suffix=['at∅'] RETOUR 0e appel de la méthode _parcours (exploration des fils du noeud o, 1/2 fils explorés) lettre ajoutée : c | suffix=['cat∅'] | ALLER 1e appel de la méthode _parcours (exploration des fils du noeud i, 0/1 fils explorés) suffix=[] | | ALLER 2e appel de la méthode _parcours (exploration des fils du noeud n, 0/1 fils explorés) suffix=[] | | | ALLER 3e appel de la méthode _parcours (exploration des fils du noeud e, 0/1 fils explorés) suffix=[] | | | | ALLER 4e appel de la méthode _parcours (exploration des fils du noeud ∅, 0/0 fils explorés) suffix=[] | | | | RETOUR Fin de mot ! | | | RETOUR 3e appel de la méthode _parcours (exploration des fils du noeud e, 1/1 fils explorés) lettre ajoutée : ∅ | suffix=['∅'] | | RETOUR 2e appel de la méthode _parcours (exploration des fils du noeud n, 1/1 fils explorés) lettre ajoutée : e | suffix=['e∅'] | RETOUR 1e appel de la méthode _parcours (exploration des fils du noeud i, 1/1 fils explorés) lettre ajoutée : n | suffix=['ne∅'] RETOUR 0e appel de la méthode _parcours (exploration des fils du noeud o, 2/2 fils explorés) lettre ajoutée : i | suffix=['cat∅', 'ine∅']
On peut remarquer un léger problème : le caractère de fin de mot ∅ est ajouté aux chaînes de caractères. C’est tout à faire normal. En effet, notre critère pour renvoyer la chaîne de caractère qui servira à reconstruire le mot lors de la remontée, est de visiter un nœud qui n’a pas d’enfants, et où la variable trie à explorer est donc {}. Or, cette condition n’est réunie que pour un nœud : le nœud ayant ∅ pour étiquette. Ainsi, cela implique à un moment de la récursion de faire un appel du type self._pacours(trie['∅'])) à la ligne 14. Or, à la ligne 14, nous ajoutons par défaut l’étiquette du nœud que nous venons d’explorer, d’où l’ajout du caractère ∅. Il existe donc deux solutions pour ne pas avoir ce caractère :
- changer le caractère de fin de mot par une chaîne vide (à faire à la construction de l’arbre dans le fichier
main.pyà la ligne 10) - changer les lignes 10 et 11 de
_parcourspar le code ci-dessous. Attention, il pas dereturn suffixdans ce cas, car un nœud peu avoir à la fois un enfant∅mais également d’autres enfants… Si nous faisions unreturnici, nous n’explorerions pas tous les enfants !
1
2
if self.end in trie:
suffix.append("")
Nous en avons donc fini avec la méthode _parcours qui ne présente pas nécessairement de difficulté particulière d’un point de vue technique, mais probablement un peu plus d’un point de vue conceptuel, si vous n’êtes pas familier de la récursion.
Aller plus loin
Voici quelques idées pour aller plus loin sur la manipulation des arbres ou sur la complétion en elle-même.
Sur les arbres
-
Créer une méthode qui permet de savoir si un mot est présent ou non dans l’arbre. Redéfinir
__contains__semble être une bonne idée. Ce va permettre d’écrire du code Python plus idiomatique par la suite, par exempleif 'William' in trieplutôt queif trie.has_word('William')qui est moins idiomatique. -
Écrire une méthode permettant de supprimer un mot. Attention, lorsqu’on supprime un mot, il faut non seulement enlever le caractère de fin de mot
∅, mais également les nœuds qui ne servent plus … mais attention a ne pas en supprimer trop. Si par exemple on souhaitait supprimer le mot « kiwis » (pluriel) il faudrait d’abord supprimer le nœud∅puis le nœudsmais pas le reste, en effet, les nœuds « k », « i », « w », « i » et « ∅ » servent encore à former le mot « kiwi » (singulier).
Sur la complétion
Notre approche est assez rudimentaire dans la présentation des suggestions, et notamment, ici les suggestions vont du mot le plus long au mot le plus court.
-
Est-ce vraiment un approche pertinente ? A priori, l’ordre des suggestions devrait non seulement être dicté par le nombre de caractères économisés (que l’utilisateur n’aura pas écrire) mais aussi par la fréquence des mots (fréquence calculé sur un corpus représentatif du français). Pour stocker la fréquence d’un mot, rien de plus simple, il suffit de le stocker dans le nœud de fin de mot
∅! -
Dans une application réelle, on suggère les mots non seulement en fonction du préfixe rentré, mais également des mots précédents. Il serait donc opportun d’ajouter un modèlé de langue pour trier la liste de suggestions en fonction de leur probabilité et du nombre de lettres économisées.
Conclusion
Nous avons réalisé un programme d’auto-complétion en Python grâce à des arbres n-aires, qui, comme nous l’avons noté, sont plus efficaces qu’une simple liste. Si vous ne connaissiez pas déjà la notion d’« arbre » en algorithmique, cet article était probablement assez dense ; je vous invite dans ce cas à le reprendre étape par étape, et pour bien faire, sans regarder la correction ![]()
Le programme complet est téléchargeable ici et est distribué sous licence Creative Commons 4.0 BY.